幂函数属于高中数学中一个重要的概念，它是由一个常数和自变量的幂次组成的函数。在数学中，幂函数可以表示为f(x)=x^n，其中n表示幂次，x表示自变量，f(x)表示因变量。在本文中，我们将探究幂函数的变化规律，从多项式到指数函数。

（一） 幂函数的基本概念与分类

1. 幂函数的定义

幂函数f(x)=x^n中，n为自然数，且n≠0，x为自变量，f(x)为因变量。幂函数可以表示为一个单相等式，即x^n=y（y>0），其中y表示幂函数的取值。

2. 幂函数的分类

幂函数可以分为多项式函数和指数函数两大类。具体分类如下：

多项式函数：幂次为正整数的幂函数，其基本形式为f(x)=ax^n+bx^(n-1)+…+k（a≠0）。

指数函数：幂次为常数的函数，其基本形式为f(x)=a^x（a>0，且a≠1）。

3. 幂函数的图像

幂函数的图像与幂次n的正负性以及系数的符号有关。当幂次为奇数时，图像经过原点并分别在第二、四象限和第一、三象限交坐标轴；当幂次为偶数时，图像经过原点且不与坐标轴交于其他点。

（二） 多项式函数的变化规律

多项式函数是一种幂次为正整数的幂函数。它的一般形式为f(x)=ax^n+bx^(n-1)+…+k（a≠0）。多项式函数的变化规律可以通过以下几个方面了解：

1. 幂次的影响

当n为奇数和偶数时，多项式函数的图像有明显的差异。当n为奇数时，函数图像以原点为对称中心呈现出“V”形，两个端点坐标的y值同号；当n为偶数时，函数图像有一个“U”形，两端点坐标的y值异号。

例如，f(x)=x^3在坐标轴上的交点为(0,0)，在第一象限和第二象限上呈现出“V”形。

而f(x)=x^4的图像则成为“U”形。

2. 符号的影响

多项式函数的符号对图像的形状和位置都会有影响。当n为奇数时，函数图像在第一象限和第三象限上为正，第二象限和第四象限上为负；当n为偶数时，函数图像在第一象限和第四象限为正，第二象限和第三象限为负。

例如，f(x)=2x^3-x^2+3的图像在第二象限和第三象限为正，第一象限和第四象限为负。

3. 参数的影响

多项式函数中各项系数的大小和符号都会对图像的形状和位置产生影响。例如，对于f(x)=2x^3-x^2+3，如果将2改为1/2，则函数图像将被压缩，而将3改为-3，则函数图像将被上移。

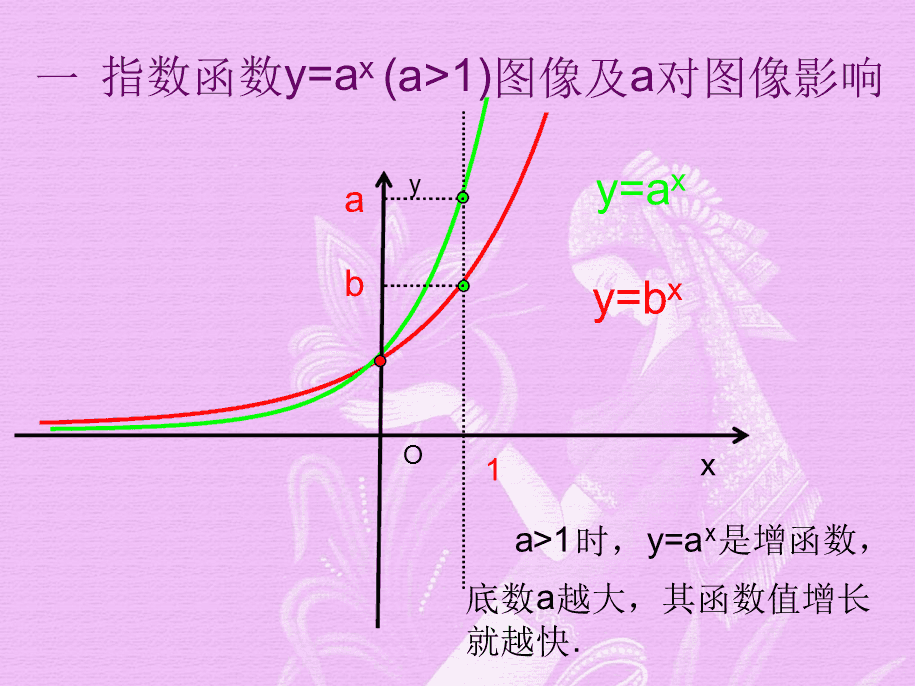
（三） 指数函数的变化规律

指数函数是幂次为常数的幂函数，其基本形式为f(x)=a^x（a>0，且a≠1）。指数函数的变化规律可以从以下三个方面入手：

1.底数的影响

指数函数中底数对图像的形状和位置产生很大的影响。当底数a>1时，函数图像在原点右侧以指数形式上升；当0

例如，f(x)=2^x的图像站在原点右侧上升，而f(x)=0.5^x的图像站在原点右侧下降。

2. 对数函数的影响

指数函数和对数函数是互相逆运算的函数，它们的函数图像也具有一定的联系。当指数函数在某点x处取值为y时，对数函数在y处取值为x。

例如，f(x)=2^x在点（1，2）处取值，则g(x)=log2(y)在点（2，1）处取值。

3. 参数的影响

指数函数中基数a和指数x的值都会对图像的形状和位置产生影响。例如，当函数f(x)=a^x中a的值增加，函数图像会左移，但y的值逐渐变大。

（四） 幂函数的应用

幂函数在数学中有着重要的应用。下面我们介绍两种常见的应用方式：

1.衰减函数

衰减函数是指形式为f(x)=a(1-r)^x（a>0，0

2.复利计算

复利是指利息在每个计息期内都被加到本金中，下一个计息期的利息就是本金和利息总和的一定比例所得的利息。复利计算可以用幂函数来表示，其一般求解公式为f(x)=p(1+r/n)^(n*x)（其中p为本金，r为年利率，n为每年计息次数，x为年数）。

（五） 结论

通过本文的探究，我们可以得出以下结论：

1.幂函数包含多项式函数和指数函数两种形式。

2.多项式函数的变化规律主要包括幂次、符号、参数等因素。

3.指数函数的变化规律主要包括底数、对数函数和参数等因素。

4.幂函数在物理、化学、生态和金融等领域都有着广泛的应用。

总之，幂函数作为高中数学中的重要概念，能够帮助我们更好地理解数学中的各种变化规律，并为我们的实际应用提供帮助。对于学生来说，理解幂函数的相关知识，对于提高数学分数和素质教育也有着重要的意义。